Bryan wrote:
David,
Forgive me if there are later posts that modify this post. I understand the distinction that you are making about where the "disproportionate" gain is. The issue I have is that your assertions are both vague and general. You don't specify what before and after balls you are comparing when you say the slopes of the lines are different. Nor do you quantify the specific difference in the slopes. You imply that they are significant, but what is significant? I'll ask you the same as I asked Garland, do you have any controlled study that you've seen that demonstrates the difference in slopes?
Unfortunately I do not have specific data for the old balls or the lower swing speeds. I recall seeing some or figuring some out at some point before but don't have it handy now. That is one of the real frustrations here . . . The USGA has all the info, but they have failed analyze that info in a meaningful way. (If they have, then they haven't provided us with with results.)
I don't have an Iron Byron, but a few years I did a test once using what I will call The Latex Lynn, a "golf machine" with a swing-speed in the mid 90 mph range. The Latex Lynn hit 50 drives on a launch monitor, half with the ProV1x and half with the Tour Balata (I intermixed and teed the balls) and I recorded the results, then threw out worst 5 from each group (the Latex Lynn is not quite as consistent as the Iron Byron.) On The Latex Lynn
the ProV1x was shorter on average (around 3 or 4 yards, if I recall correctly) than the Tour Balata. (This was the case even though the Balatas were probably at least six or seven years old.)
I'd also question your statement (that I've highlighted in red above) that you took a huge hit in distance going to a Pro V1. How huge a hit did you take? What ball were you using before? I've never heard anyone assert before that they lost distance with the Pro V1.
That was a mistake on my part. "I" was writing from the perspective of "EIGHTY" (believe it or not my swingspeed is higher than that) and I probably should have written ProV1x. As for me, I do take a noticable hit with the ProV1x even compared to the ProV1 but I could not quantify it. As for the ProV, I don't think I've gained any distance (and possibly lost a bit) but cannot be certain. Anecdotally, I hit the Balata further than the ProV1x as well, but did not difference the amount.
I agree that you could regulate both the max distance and the slope. It would be relatively easy to set the targets, as you say. But, it would be harder to specify the testing procedure. For instance, what launch conditions would you propose for the conformance test? For all launch conditions? What club would you specify?
It would be hard to pick the procedures, but no harder than now. I am no expert on the advantages and disadvantages of the various options-- I am neither an engineer nor a scientist, and am looking at this from a theoretical perspective only. I'd have to speak to some engineers and scientists to figure it out. But whatever method was chosen, I think that also regulating the slope would go a long ways toward making the test procedures much harder to get around. Of the top of my head I would tend toward focusing on initial velocity and "optimal" spin rate and launch angle rather than trying to recreate a shot with a particular club. For example, the USGA should tell Titleist that it is going to send ProV1z flying at X mph and optimium spin and launch angle conditions (whatever spin and launch angle maximizes distance) and that the ProV1z better not fly more than Y yards or the USGA will reject it.
The engineering and manufacture of a conforming ball would, I think, be an enormous task.
I am not so sure. If we use past performance results to set our limits, then it is not exactly as if we are asking them to reinvent the wheel. And what I like best about this approach is does not dictate exactly what the companies should do, but gives them an incentive to compete. They can engineer and manufacture new products to their hearts' content, so long as they comply. That way, the manufacturers can still try to sell us new product every year and still pretend that their brand is significantly better than the others. Also, it may not be possible for a single ball to hug the slope line from the beginning to end, so manufacturers might have an incentive to build balls optimized to particular swing speeds (some are sort of heading this way, at least in marketing.)
So, can you be more specific about what you think the ideal compression target should be so that the slow speed swinger and high speed swinger of the same handicap can play the same course from the same tees and interact with the architecture in the same way? If 60 to 80 yards is too much of a delta, what delta would you like to regulate between, say a 80 mph and a 120 mph swing speed? Do you have any factual evidence of what the delta was in the '90's or earlier?
Anecdotally, I played competitive amateur golf as far back as the '60's and as far as I recall the long hitters were significantly (30 to 40 yards) longer than I was, and my swing speed was a bit above average in those times (when I was younger and stronger).
I cannot. I don't have the data. But it ought to be easy enough for the USGA to do by looking at how the past balls performed at different swing speeds. Big hitters have always had a big advantage and that is how it should be, but the goal should be twofold: 1) Push back on the big hitters enough so that they fit on courses of reasonable length, and 2) regulate the relative advantage of the big hitters back to something more in line with what it has been historically.
I don't see it as being that complicated, provided the data is available.
I don't think that David and Garland are suggesting that the modern ball is exponentially longer. It is linear, just maybe at a different slope than the balata balls of yore.
I am NOT suggesting that any particular modern ball is exponentially longer, but think that if we took looked a theoretical "OPTIMAL BALL" which represents each "state of the art" ball (distance wise) at every swing speed, then we would see something that might look like exponential distance gain, if only for a limited range of swing speeds.
Here is a chart I created a few years ago to demonstrate what I mean. The small straight lines represent slopes of particular ball types, while , the purple curved line represents our defined OPTIMAL BALL (an amalgamation made of each best ball at every swing speed.) One can see how that "exponential distance gain" could exist even if not produced by a single ball. This approach makes more sense to me, because the reality is that our swing speeds are fairly constant, and when comparing relative advantage we ought to be realistic and use the best ball at every swing speed. THIS IS FOR DEMONSTRATION PURPOSES ONLY. I don't know that this circumstance exists, but given how steep the slope is at high speeds for balls like the the BALL A above, I'd be willing to bet the that slope of the OPTIMAL BALL gets steeper in this range. theoretical, but something that the USGA could easily test and confirm (or disprove) if the so chose. [Note that for simplicity my slope lines do not taper off, but the concept is the same even with tapered slope lines.]
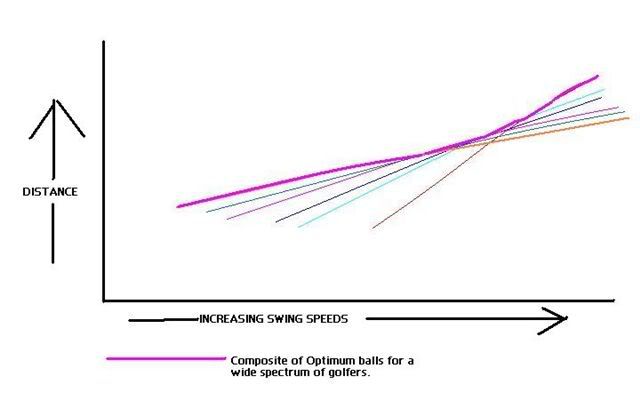
_________________________________________________________________
Garland,
That's EXACTLY what we saw when we did our USGA/R&A ball testing. My wife Laura with her 70mph driver swing speed GAINED distance when using the rolled back ball.
I'm around 95mph, and I lost about 5 yards (who cares), but I liked the additional spin on the ball, which ironically was a Bridgestone-made ball that was roughly the same as thier e5 line.
Dan
Now THAT is what I am talking about! The impact of regulating the ball does not have to kill shorter hitters, and it may even help the slowest ones out a bit.
What is better for the game in the long run . . . . building balls that don't help anyone but those that already hit drives 330 yards or building balls that might give the 70 mph swinger a little extra pop?