[David said:]
One last time. My position is that long hitters have disproportionately benefited from balls like the ProV1x, relative to short hitters.
David, I'm not sure I follow this. And I've read the many posts on the subject. Is this not the opposite of what the USGA study shows. Does their study not show that the ProV1x is actually disproportionately shorter at higher swing speeds? Can you rephrase your position to make it clearer?
Bryan, I donít think the USGA addressed what I have been saying. What they have done is offer evidence that, for each ball tested, the incremental distance increase declines per unit increase in swing speed. In other words, the slope of the line slightly flattens as speed increases. But this conclusion has little or no bearing on
whether or not long hitters have disproportionately benefited from technology, relative to short hitters. As opposed to reinventing the wheel, Iíll draw on heavily on a few of my older posts explaining the distinction, including post #24 in this thread and a post from a few months ago, when TEPaul first reported that the USGA told him that the distance progression for each ball was largely linear. . . .
In the article, the USGA charts the distance each ball travels when hit by a driver through a range of swing speeds. But when driving the golf ball, players are pretty much locked into their maximum effective swing speed, at least at given time-- No one can simply decide to just swing faster than they are capable of swinging! So while the USGA draws conclusions based on looking how a single ball performs over a series of swing speeds, I am taking it a step further--
how does each ball relatively benefit different golfers with different swing speeds? I have repeatedly proposed that
some of the newer balls (such as the ProV1x) have benefited the fast swingers more than they have benefited the slow swingers, thus creating a enlarged distance gap between fast and slow swingers. This has absolutely nothing to do with whether the slopes of these ballsí distance curves diminish, increase, or remain constant, but has everything to do with comparing the different distance characteristics (slopes) of different balls.
Let me put it this way. Say we have a fast swing golfer (say 130 mph) and a slow swing golfer (say 70 mph) who both switch to the ProV1x from the ProV1 (or even from some low-priced "distance" ball.) I think that the 130 mph golfer will benefit much more from the switch than the 70 mph golfer. By merely demonstrating that the slope of these ballsí distance curves flatten as speed increases says nothing about whether two different golf balls have different slopes and values across a range of distances.
Here is a chart I made long ago, not as evidence of any particular ball's performance, but to graphically demonstrate the point I am trying to make. I use
TWO HYPOTHETICAL BALLS, one ballís distance increases 9 yards per 5 mph increase in swing speed, the other ballís distance increases 11 yards per 5 yd increase in swing speed. Rather than redoing my chart,
and because it is irrelevant to my point, Iíll ask you to assume that these slopes are actually decreasing slightly over time at approximately the same rate (so my chart would still look like an X but with the lines both bending down at approx the same rate.)
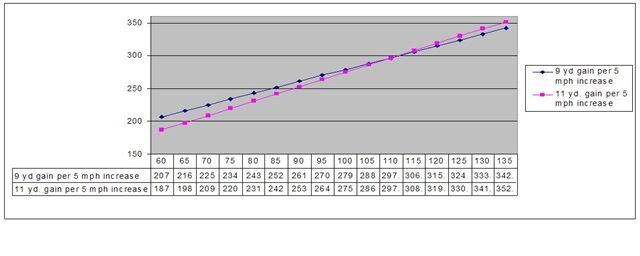
Note that the second ball greatly benefits the faster swing golfer and actually hurts the slower swing golfer, relative to the first ball. Note also that
while this is a hypothetical, it demonstrates that my premise (some balls provide greater distance benefits to fast swing golfers while not helping golfers with slow swing speeds) does NOT depend upon the slope of any ball's distance curve increasing.
Think of our conversations regarding the ProV1x. My theory is that while the ProV1x greatly benefited those with fast swing speeds, it would not similarly benefit those with slower swing speeds.
I hope this clears it up for you.